Resolution is one of the most commonly misconstrued and improperly defined descriptions of performance [1]. Misconceptions include the role of temporal and spatial bandwidth, the effects of filtering, and central effects related to detector noise, physical optics, and aberrations.
A contributor to the misunderstanding is lack of precision in the definition of the word “resolution”. In optical imaging, resolution denotes the ability to plainly distinguish between closely spaced points or features, frequently according to boundaries established by physical optics. In distance and surface height measuring systems, resolution is restricted by digitization or measurement noise. To properly understand the parameters of resolution and how to characterize them, one needs to look at these two concepts individually, and perhaps modify one’s vocabulary accordingly.
Radius of Curvature Metrology with high precision using Fizeau Interferometers
With densely-sampled images, limitations are encountered based on diffraction or optical quality that limits the ability of instrumentation to resolve closely-spaced image characteristics [2]. Lateral resolution is the smallest center-to-center separation of characteristics that still allows one to see plainly that there are two characteristics present [3]. Figure 1 shows two trenches formed by patterning silicon on a quartz substrate. The interference microscopy 3D image shows that two lines are indeed present, although they seem blurred at this high magnification. As the center-to-center separation between the lines decreases, the optical resolving power of the instrument becomes a limiting factor in defining whether the two lines are clearly divided.
Latest laser Fizeau interferometers have cameras with more than 5 million pixels, providing a comprehensive lateral sampling of form, waviness, and surface texture [4]. The topography image in Figure 2 is for a diamond-turned disk with a surface height range of a few tens of nanometers. To make the most of these large-format cameras, the optical system must be of suitable quality, with large limiting apertures.
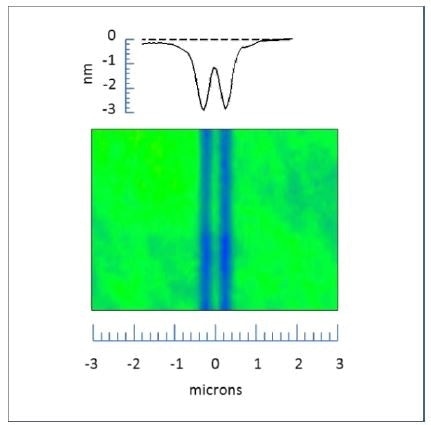
Figure 1. 3D interference microscope image of parallel trenches using a 100× objective with an NA of 0.85. The trenches are 200 nm wide and the center-to-center spacing is 440 nm
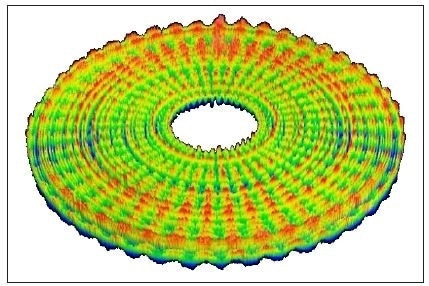
Figure 2. 3D image of a diamond-turned disk using a 100 mm aperture laser Fizeau interferometer.
It is common to quantify the lateral or imaging resolution of an instrument in terms of a single number, such as the Rayleigh limit [5]. Although more hard to specify, the modulation transfer function (MTF) and its analog, the instrument transfer function (ITF) in 3D metrology, provide much better information concerning instrument response as a function of line separation [6].
A simple linear ITF catalogs the reaction of the system to pure surface sine wave patterns as a function of frequency. In the limit of small amplitude (<<λ) or low frequency sine waves, one can predict the instrument reaction to the total surface structure by mapping the Fourier components of the surface, weighted by the ITF, to the reported topography [5]. A smart feature of the ITF characterization is that it corresponds narrowly to the power spectral density (PSD) assessment of surface error in optical fabrication [7]. The foundations for a rigorous understanding of the MTF and the linear ITF are well recorded in the literature [8]. More comprehensive models allow for spreading these ideas more generally to larger steps and slopes in coherence scanning 3D microscopy [9, 10].
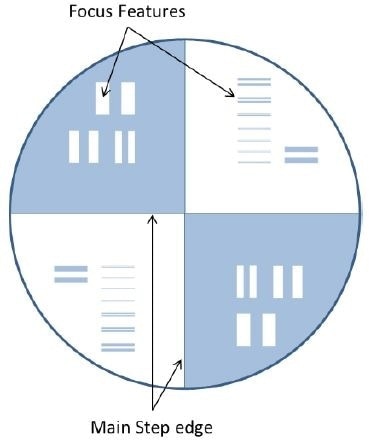
Figure 3. Patterned surface of an ITF measurement specimen with etched features for evaluating the edge spread function.
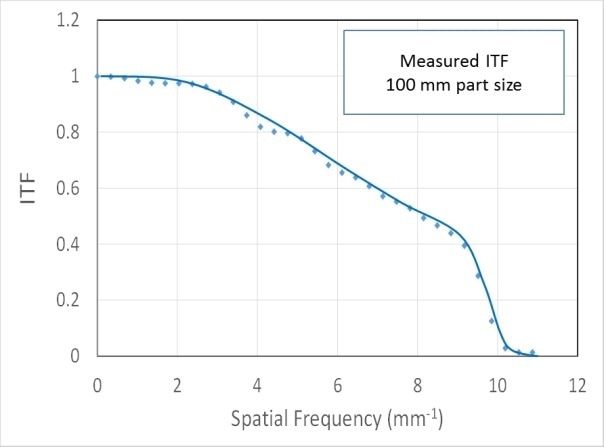
Figure 4. Example precision ITF measurement results showing a design resolution limit of 0.0625 mm or 1600 cycles/aperture.
For the measurements of ITF, the researchers use the 3D equivalent of the edge spread function [11], depending on 25 nm sharp step features across the 100 mm full aperture of a super-polished disk. The test sample illustrated in Figure 3 has both a vertical and a horizontal edge, and extra targets to aid in correctly focusing the instrument. The ITF calculation follows from comparing the frequency content of the measured step to an idealization of an ideal step.
Figure 4 illustrates an ITF measurement result, in this case for an instrument with a design maximum spatial frequency of 16 cycles/mm. Measurements at different field positions confirm that the predicted spatial frequency response is uniform over the total surface area. The steep slope at high frequencies is steady with apertures in the optical system meant to prevent camera aliasing [12].
A crucial aspect of imaging resolution is that it relates to central physical principles that have little to do with measurement noise. The image in Figure 1 can be averaged for days, and perhaps gain an additional 10% in resolution just from the better quality of the image. But eventually, the limitations of the imaging principle, the wavelength, and the apertures within the optical system take over. Similar restrictions apply to depth discrimination in confocal microscopy and optical coherence tomography. These restrictions do not apply, at least not in the same way, to the following topic.
Resolution in Distance Measurements
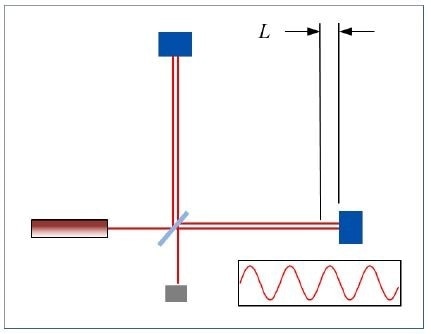
Figure 5. Interferometer for measuring the distance L.
Optical dimensional metrology usually involves one or more distance, displacement or surface height measurements in relation to a virtual reference point or plane in space. Figure 5 illustrates an interferometric sensor for measuring a distance or displacement L. The smallest detectable variation δL is frequently called the “resolution”. Of note, δL is not associated with the separation of two object points or distances at the same time, as in imaging resolution. As such, there is no absolute physical limit regarding how small δL can be. There is no Airy spot with which to contend as a fundamental limit.
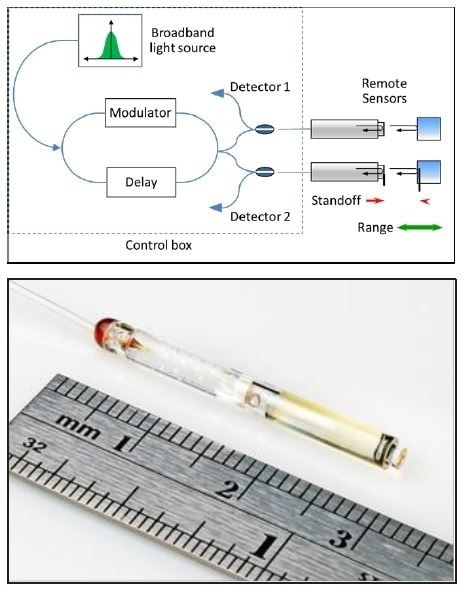
Figure 6. High-precision, fiber-based position sensing system [13, 14].
Assuming that there is a surplus of digitization for recording fine increments, the “resolution” of distance sensors is equal to random measurement noise. Accordingly, proper specification essentially includes the bandwidth or measurement time [1]. It also follows that with adequate light source power, time, and signal to noise, there is no lower limit to what is attainable in detector sensitivity. Latest precision sensors such as the fiber-based device illustrated in Figure 6 have 3σ noise figures in the 0.5 nm range at 10 kHz, compared to >250 nm limit for the lateral resolution in visual wavelength microscopy.
TABLE 1. Specifications for the precision sensing system shown in FIGURE 6.
| Fiber sensor specifications [15] |
| Digital Resolution |
0.01 nm |
Noise (3σ) |
0.005 nm/√Hz |
| Data Rate |
Max 208 kHz |
Stability |
1 nm / day |
| Channels |
Up to 64 |
Non-linearity |
± 1 nm |
Resolution in Surface Topography
Areal surface topography offers a stimulating and sometimes confounding mixture of the two resolution concepts mentioned here. The measurement in 3D measuring microscopy offered by interferometers, confocal, and focus variation instruments is a collection of height measurements over an imaged surface area. The ability to isolate features on the topography map is connected to imaging resolution, while the change in surface height that one can detect is ruled by measurement noise. It is unfortunate that the term “vertical resolution” is extensively used for such instruments, as it encourages confusion of the two concepts. This is apparent in specification sheets for these instruments, which, with few allowances, make no mention of time bandwidth or measurement speed when quoting vertical resolution [16]. Draft ISO standards for calibration will maybe mandate a correction to this practice [17].
Apart from model-based approaches comparable to scatterometry and improvements to image clarity and correction for undersampling, 3D interference microscopes continue to be diffraction limited. Surface height “resolution”, in contrast, has room to advance based on quantum well depth, data acquisition speed, and camera pixel count. The present state of the art for interference microscopy, for instance, provides better than 0.1 nm/√Hz over one million simultaneous height measurements [18]. Following the familiar √N rule means that a 10 nm repeatability is attainable in 100 seconds. It is rational to consider approaches and enabling technologies that can decrease this even further without breaking any major limits.
The Limits of Resolution
Here the author has debated that characterizing the restrictions of resolution requires a modification in one’s vocabulary. It would be preferable in specification sheets and technical reports to reserve “resolution” for those metrology features that are controlled by one’s ability to plainly separate adjacent features or surface depths, as in 2D and 3D imaging. For distance measurements, including height measurements for broadly-separated surface features, it would be better to quantify the measurement noise or the equivalent, taking into consideration if it is a single standard deviation or a multiple thereof.
Once everyone is talking the common language, there is a broad range of advantageous characterization methods. For imaging resolution, sample specimens with closely-spaced characteristics complement linear ITF techniques based on the edge spread function and other techniques. For distance measurements, the corresponding noise levels can typically be established from repeatability tests over a variety of bandwidths. These characterization techniques allow for advances in performance, sensible comparison of instrumentation, and adaption of measurement methods to challenging applications.
Acknowledgements
The authors recognize the contributions of ZYGO scientists and engineers to the results shown in this paper. We also thank Prof. Richard Leach for his review of the draft manuscript.
References
- Understanding Sensor Resolution Specifications and Performance. Lion Precision TechNote. 2014:
- de Villiers, G., and Pike, E. R. The limits of resolution. CRC Press, Boca Raton, 2017.
- ISO DIS 25178-600:201: Geometrical product specifications (GPS) - Surface texture: Areal - Part 600: Metrological characteristics for areal-topography measuring methods (DRAFT 2017-03-29) International Organization for Standardization, Geneva 2017.
- Sykora, D. M., and de Groot, P., Instantaneous measurement Fizeau interferometer with high spatial resolution. in Optical Manufacturing and Testing IX, Proc. SPIE. 2011; 8126: 812610-812610-10.
- de Groot, P., Colonna de Lega, X., Sykora, D. M. et al. The Meaning and Measure of Lateral Resolution for Surface Profiling Interferometers. Optics and Photonics News. 2012; 23: 10-13.
- de Groot, P., and Colonna de Lega, X., Interpreting interferometric height measurements using the instrument transfer function. in 5th International Workshop on Advanced Optical Metrology, Proc. FRINGE Springer Verlag. 2006; 30-37.
- ISO 10110-8:2010(en), Optics and Photonics – Preparation of drawings for optical elements and systems International Organization for Standardization, Geneva 2010.
- Goodman, J. W. Introduction to Fourier Optics. McGraw-Hill, New York, 1996.
- Coupland, J., Mandal, R., Palodhi, K. et al. Coherence scanning interferometry: linear theory of surface measurement. Applied Optics. 2013; 52: 3662-3670.
- Su, R., Wang, Y., Coupland, J. et al. On tilt and curvature dependent errors and the calibration of coherence scanning interferometry. Optics Express. 2017; 25: 3297-3310.
- Takacs, P. Z., Li, M. X., Furenlid, K. et al. Step-height standard for surface-profiler calibration. Proc. SPIE, 1993; 1995: 235-244.
- Deck, L. L. Method and apparatus for optimizing the optical performance of interferometers. US patent number Application 15/383,019. 2016.
- Badami, V. G., Wesley, A. D., and Selberg, L. A., A high-accuracy, multi-channel, fiber-based displacement/ distance measuring interferometer system. in Annual Meeting of the American Society for Precision Engineering, Proc. ASPE ASPE. 2013;
- de Groot, P., Deck, L. L., and Zanoni, C. Interferometer system for monitoring an object. US patent number 7,636,166. 2009.
- de Groot, P., The meaning and measure of vertical resolution in surface metrology. in 5th International Conference on Surface Metrology, Proc. ICSM. 2016;
- ISO WD 25178-700.2: Geometrical product specifications (GPS) - Surface texture: Areal - Part 700: Calibration and verification of areal topography measuring instruments (DRAFT) International Organization for Standardization, Geneva 2017.
- Fay, M. F., Colonna de Lega, X., and de Groot, P., Measuring high-slope and super-smooth optics with high-dynamic-range coherence scanning interferometry. in Optical Fabrication and Testing (OF&T), Classical Optics 2014, OSA Technical Digest. 2014; paper OW1B.3.

This information has been sourced, reviewed and adapted from materials provided by Zygo Corporation.
For more information on this source, please visit Zygo Corporation.