Micropillar compression testing [1] is fast emerging as a viable alternative to nanoindentation, for the measurement of mechanical properties and deformation behavior of small volumes and thin films. This technique has been used with a number of materials, including ceramics, polymers, and metals.
Generally, FIB milling – or etching, in the case of ceramics and metals – is used on pillars which are micron-sized. Subsequently, the pillars are compressed, and the stress-strain properties of compression are measured using a flat punch.
Using a flat punch to exchange the widely used pyramidal tips, a nanoindenter can be used to make measurements. Inside the SEM, precise positioning of the flat punch on the micropillar can be enabled with in-situ testing. This allows for observation of deformation, which is frequently not possible when using ex-situ testing as a result of errors associated with tip-to-optic calibration.
Yet, in-situ testing in an electron microscope is not an option for a number of material classes such as cements and polymers. This is because of cracking and beam damage. Consequently, the alignment and precise positioning of the indenter flat punch on the micropillar is desired. This is achieved with the use of an optical microscope.
The intention of this article is to demonstrate the micropillar compression of polymeric fibers under an optical microscope with the use of an Alemnis indenter.
Experimental
For this study, high-speed melt-spun cyclo-olefin polymer (COP) and copolyamide (CoPA) polymers were chosen – as well as polyamide 66 and polyethylene terephthalate (PET).
A specimen preparation technique which was previously developed by Leal et al. [2] was the basis of the preparation of fiber specimens suitable for axial compression. The prepared free standing polymeric specimen is illustrated by the electron micrograph in Fig. 1. This is suitable for a single fiber axial micro-compression test.
An Alemnis nanoindenter (Alemnis AG) was used to determine the axial compressive modulus of single filaments. This is a modified, up-to-date version of the in-situ indenter which was first developed by Rabe [3].
In order to apply a uniform axial compressive load to the fiber specimens – which have a diameter of 70‐90 μm – a flat punch indenter of 200 μm diameter was used. Aided by the use of a Keyence VH-Z100R optical microscope for compression, the flat-tipped indenter was placed carefully over a single fiber specimen.
After positioning the flat-tipped indenter over the single fiber specimen, the axial micro-compression test is performed by applying the compressive load at a constant rate of extension until a pre-defined maximum displacement value is reached.
Following this, the tip is retracted until its original position is reached. A rate of 0.5 μm/s was used to test the specimens. Indents on fused silica of known modulus value were used to determine the system compliance.

Figure 1. Electron micrographs of COPa fiber specimens before and after microcompression up to 20 percent strain.

Figure 2. (a) Experimental set‐up comprising of an Alemnis indenter used under a Keyence optical microscope for microcompression of polymer fibers, and (b) optical image of a fiber during compression with a flat punch.
Results and Discussion
Generally exhibiting reduced performance under compression in relation to their tensile behavior, polymer filaments are anisotropic materials [2]. Fig. 3 (a) shows typical stress-strain curves in axial compression for the varying monofilaments of interest.
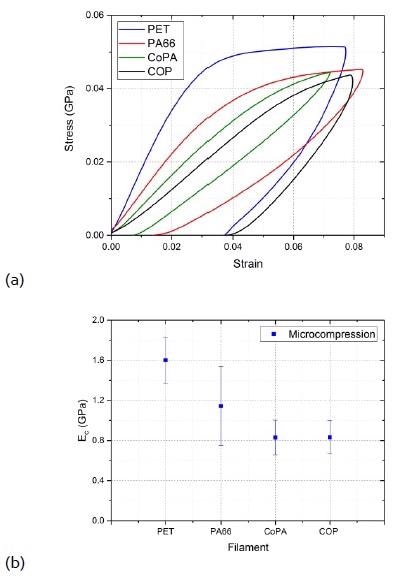
Figure 3. (a). Stress‐strain curves in axial compression for different melt‐spun monofilaments, and (b) Axial compressive modulus for different melt‐spun filaments. Ec values are the average of 8 to 12 measurements. Error bars represent the standard deviation.
Freestanding single filaments with aspect ratios (length/radius) between 1.5 and 6.5 were yielded by the specimen preparation technique. As the specimens do not follow Euler’s buckling behavior, the stress-strain curves were used to directly determine the axial compressive moduli.
As illustrated in Fig. 3 (a), maximum compressive strains of the order of between 0.07 and 0.08 were applied to the filaments. An obvious transition into plastic deformation is witnessed from the PA66 and PET curves for these strain levels.
Meanwhile, CoPA and COP seem to stand on the boundary between plastic and elastic deformation. Fig. 3 (b) illustrates the measured axial compressive modulus values for PA66, PET, COP, and CoPA filaments.
The PA66 specimens have a relatively large standard deviation, with a 34% coefficient of variation. A student’s t-test of hypothesis with a significance level of α=0.1 suggests that the mean modulus value of PA66 is statistically different than those of COP, CoPA, and PET.
Despite this, the PA66 error bar (±1 standard deviation) does substantially overlap with those for COP, CoPA, and PET. The compressive modulus value of PET is nearly 30% higher than the observed value for PA66, and approximately 50% higher than those for the amorphous COP and CoPA polymers – as shown in Fig. 3 (b).
Figure 3. (a). Stress-strain curves in axial compression for different melt-spun monofilaments, and (b) Axial compressive modulus for different melt-spun filaments. Ec values are the average of 8 to 12 measurements. Error bars represent the standard deviation.
When compared to other polymer textile fibers, it is well known that PET filaments have a greater stiffness [4, 5]. One of the most significant parameters which affects the compressive properties of polymer fibers is the fact that they can form lateral intermolecular interactions. In the majority of cases, this consists of a secondary type of bonding.
For PET, aromatic rings usually stack regularly in the crystalline domains, which gives place to secondary bonding through aromatic ring association [5]. Conversely, PA66’s flexible aliphatic polymer chain structure leads to reduced stiffness values in relation to PET.
Nevertheless, PA66’s ability to establish the strongest type of secondary bonding between amide groups of adjacent polymer chains [6, 7] (intermolecular hydrogen bonds), enables a compressive modulus value which is 30% lower than PET to be achieved by the filament. Meanwhile, the tensile modulus of the PA66 filament is 70% lower than PET.
On the contrary, the amorphous CoPA and COP polymers are designed in such a way as to have inherent characteristics which hinder the development of the molecular order which is needed to achieve high modulus values (as well as other things).
Conclusions
In summary, an Alemnis nanoindenter was used to carry out the microcompression of free standing polymeric fibers. Their compressive elastic moduli were also measured. The compressive response of various melt-spun amorphous filaments can be quantified using this experimental methodology.
This article demonstrates the Alemnis nanoindenter’s versatility and flexibility, which can be utilized together with other techniques, such as optical microscopy.
References
[1] Uchic MD, Dimiduk DM. A methodology to investigate size scale effects in crystalline plasticity using uniaxial compression testing. Materials Science and Engineering: A 2005;400:268‐78.
[2] Leal AA, Deitzel JM, Gillespie JW. Assessment of compressive properties of high performance organic fibers. Composites Science and Technology 2007;67:2786‐94.
[3] Rabe R, Breguet J‐M, Schwaller P, Stauss S, Haug F‐J, Patscheider J, et al. Observation of fracture and plastic deformation during indentation and scratching inside the scanning electron microscope. Thin Solid Films 2004;469:206‐13.
[4] Naskar AK, Mukherjee A, Mukhopadhyay R. Studies on tyre cords: degradation of polyester due to fatigue. Polymer Degradation and Stability 2004;83:173‐80.
[5] Perepelkin K. Physicochemical nature and structural dependence of the unique properties of polyester fibres. Fibre Chemistry 2001;33:340‐52.
[6] Atkins EDT, Hill M, Hong SK, Keller A, Organ S. Lamellar structure and morphology of nylon 46 crystals: a new chain folding mechanism for nylons. Macromolecules 1992;25:917‐24.
[7] Colomban P, Sagon G, Lesage M, Ramirez JMH. Micro‐Raman study of the compressive behaviour of advanced PA66 polyamide fibres in a diamond‐anvil cell. Vibrational spectroscopy 2005;37:83‐90.
This application note is based on the paper “Mechanical response of melt‐spun amorphous filaments” published in Science and Technology of Advanced Materials 15 (2014) 035016 DOI: 10.1088/1468‐6996/15/3/035016 Authors: A. Andres Leal, Gaurav Mohanty, Felix A. Reifler, Johann Michler and R. Hufenus
A. Andres Leal, Guarav Mohanty, Felix A. Reifler, Johann Michler, and R. Hufenus
Empa – Swiss Federal Laboratories for Materials Science and Technology

This information has been sourced, reviewed and adapted from materials provided by Alemnis AG.
For more information on this source, please visit Alemnis AG.