Measuring the Complex Modulus of Highly Plasticized Polyvinyl Chloride via Instrumented Indentation

Polymers are often employed in engineering designs because of their ability to damp out shock and vibration. A material’s ability to elastically store energy is characterized by the storage modulus (E’); the ability to damp is characterized by the loss modulus (E”). The complex modulus (E*) is often used to characterize polymers because it incorporates both of these capacities: E* = E’ + iE”.

For bulk samples of material, complex modulus can be measured using dynamic mechanical analysis (DMA). The sample is oscillated in tension, compression, or bend, and the complex modulus is determined from the sample’s response to the oscillation. Several commercial vendors offer equipment for making such large-scale measurements using DMA. KLA nanoindentation systems equipped with the Continuous Stiffness Measurement option offer the ability to oscillate the indenter. In this way, the complex modulus can be determined from a proper analysis of the contact [1–3].

Instrumented indentation, also known as nanoindentation, offers two important advantages over DMA when measuring complex modulus. First, the measurement can be made on a spatially resolved scale, thus allowing one to map out the complex modulus as a function of position. Second, because the moving mass in a nanoindentation system is smaller, the resonant frequency of the equipment is higher, thus allowing a larger frequency range for testing.

In the work discussed herein, dynamic instrumented indentation is employed to measure the complex modulus of highly plasticized polyvinyl chloride (PVC). Results from this work are compared with previously published results for the same material [4–6].

For a thorough literature review and a complete treatment of the theory behind measuring complex modulus by dynamic indentation, please consult reference [4]. We have applied this theory to both the equipment and the contact in order to derive expressions for the complex modulus in terms of quantities that are measured during a dynamic indentation experiment [7].

Indenter Schematic

KLA G200 nanoindentation systems can be properly represented by the schematic shown in Figure 1. Semi-static and dynamic forces are imposed electromagnetically. The indenter column is supported by two “leaf” springs that are laterally stiff, but compliant in the direction of indentation. Displacement is measured using a three-plate capacitive arrangement. All three plates are circular disks. The two outside plates are fixed to the head and have holes in the center just large enough to accommodate the indenter shaft. The center plate is fixed to the indenter shaft and is free to move vertically between the two outside plates. The position of the indenter column within the gap is determined by observing the voltage between the center plate and either of the two outside plates.

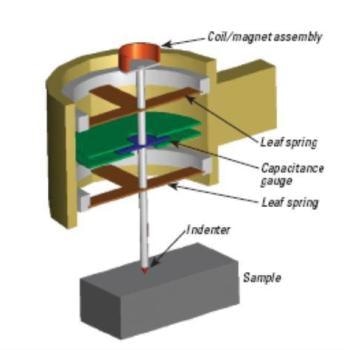
Figure 1. Schematic of the “head” of a KLA Nano Indenter system.

Experimental Method

The highly plasticized PVC tested in this work is a product of 3M (EAR C-1002-25). The material is used to provide damping under and around heavy rotating equipment. The material arrived in a small square sheet, approximately 6 inches on a side and ¼-inch thick. One side of the sheet was mechanically polished to remove a surface layer. Then a 1-inch square was cut from the sheet and mounted on an aluminum puck as shown in Figure 2.

Figure 2. Highly plasticized PVC (3M EAR C-1002-25) mounted for testing.

A KLA Nano Indenter G200 with Continuous Stiffness Measurement option and XP-style actuator was used for all testing. The indenter tip was a flat-ended cylindrical punch made of diamond. The punch, shown in Figure 3, had a diameter of 107.1 microns. The advantage of a flat-ended punch for this testing is that the contact area is constant, and not a function of contact depth.

Figure 3. Flat-ended cylindrical punch tip (XP-style holder, 107.1µm diameter).

The KLA NanoSuite test method “G-Series XP Continuous Stiffness Measurement Flat Punch Complex Modulus” was used for this work. This test method brings the indenter into full contact with the test material, oscillates the indenter over a range of frequencies, and then applies the analysis. Each test yields complex modulus as a function of frequency for a specific test site. Fourteen tests at fourteen different sites were performed. User-defined inputs were selected to match the test conditions reported by Herbert et al. for the same material [4–5]. Tests were conducted at room temperature.

Results and Discussion

Results for storage modulus and loss factor are shown in Figures 4 and 5. Error bars on the symbols represent one standard deviation on the average.

Figure 4. Storage modulus as a function of frequency as determined by default and in situ calibration. Results from this work are compared with previously published results obtained by indentation and DMA [4].

Figure 5. Loss factor as a function of frequency as determined by default and in situ calibration. Results from this work are compared with previously published results obtained by indentation and DMA [4].

These figures compare the results of the present work with those obtained by Herbert et al. [4–5] for the same material. Herbert et al. employed both DMA (TA Instruments) and indentation (KLA XP Nano Indenter). For the indentation testing, they used a flat-ended punch of similar diameter (~100 microns). They used a custom indentation test method that was not commercially available.

The agreement between the present results and the indentation results reported by Herbert et al. is excellent. Slight differences, especially at 50 Hz, may be explained by the slightly higher temperature for the present results because the properties of this material are a strong function of temperature [5].

Given the profound differences in test method and sample geometry, the agreement with DMA is also outstanding. The “wobble” in the DMA results at higher frequencies is likely due to an inadequate accounting for instrument influence, although Herbert et al. report that the instrument was calibrated according to the manufacturer’s instructions.

The resonant frequency of the instrument (whether DMA or indentation) depends inversely on the moving mass. That is, a larger moving mass means a lower resonant frequency. At testing frequencies greater than the resonant frequency, the instrument response becomes progressively more influential – the dynamic stiffness of the instrument increases sharply. Accurately predicting this response becomes progressively more important. Therefore, a testing instrument with a smaller moving mass offers definite experimental advantages.

Conclusions

The KLA Nano Indenter G200 was successfully used to measure the complex modulus of highly plasticized polyvinyl chloride. Results agreed well with those obtained by others using dynamic mechanical analysis (DMA) and dynamic indentation. Dynamic indentation offers distinct advantages over DMA. First, complex modulus can be measured locally for small volumes of material. Second, instrument calibration is less critical because a smaller moving mass means that the instrument has a smaller influence on the measurements.

References

[1] I.N. Sneddon, “The relation between load and penetration in the axisymmetric Boussinesq problem for a punch of arbitrary profile,” Int. J. Eng. Sci., Vol. 3, pp. 47–56, 1965.

[2] W.C. Oliver and G.M. Pharr, “An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments,” J. Mater. Res., Vol. 7 (No. 6), pp. 1564–1583, 1992.

[3] J-L. Loubet, B.N. Lucas, W.C. Oliver, “Some measurements of viscoelastic properties with the help of nanoindentation,” NIST Special Publication, Vol. 896, pp. 31–34, 1995.

[4] E.G. Herbert, W.C. Oliver, G.M. Pharr, “Nanoindentation and the dynamic characterization of viscoelastic solids,” J. Phys. D: Appl. Phys., Vol. 41, pp. 1–9, 2008.

[5] E.G. Herbert, W.C. Oliver, A. Lumsdaine, G.M. Pharr, “Measuring the constitutive behavior of viscoelastic solids in the time and frequency domain using flat punch indentation,” J. Mater. Res., Vol. 24 (No. 3), 2009.

[6] http://en.wikipedia.org/wiki/Polyvinyl_chloride

[7] J.L. Hay, P. Agee, E.G. Herbert, “Continuous stiffness measurement during instrumented indentation testing,” Experimental Techniques, January 2010.
First page: http://dx.doi.org/10.1111/j.1747- 1567.2010.00618.x

This information has been sourced, reviewed and adapted from materials provided by KLA Corporation.

For more information on this source, please visit KLA Corporation.

Disclaimer: The views expressed here are those of the author expressed in their private capacity and do not necessarily represent the views of AZoM.com Limited T/A AZoNetwork the owner and operator of this website. This disclaimer forms part of the Terms and conditions of use of this website.