| Optical tweezers use light to manipulate microscopic objects as small as a single atom. The radiation pressure from a focused laser beam is able to trap small particles. In the biological sciences, these instruments have been used to apply forces in the pN-range and to measure displacements in the nm range of objects ranging in size from 10 nm to over 100 mm. How Do Optical Tweezers Work? The most basic form of an "optical trap" is diagramed in Figure 1a - see below. A laser beam is focused by a high-quality microscope objective to a spot in the specimen plane. This spot creates an "optical trap" which is able to hold a small particle at its center. The forces felt by this particle consist of the light scattering and gradient forces due to the interaction of the particle with the light (Figure 1b, see details below). Most frequently, optical tweezers are built by modifying a standard optical microscope. These instruments have evolved from simple tools used to manipulate micron-sized objects, to sophisticated devices under computer-control that can measure displacements and forces with high precision and accuracy. | | | Figure 1a and 1b. The principles of how Optical Tweezers work. | Industry Applications for Optical Tweezers Optical tweezers have been used to trap dielectric spheres, viruses, bacteria, living cells, organelles, small metal particles, and even strands of DNA. Applications include confinement and organization (e.g. for cell sorting), tracking of movement (e.g. of bacteria), application and measurement of small forces, and altering of larger structures (such as cell membranes). Using Optical Traps to Study Molecular Motors and the Physical Properties of DNA Two of the main uses for optical traps have been the study of molecular motors and the physical properties of DNA. In both areas, a biological specimen is biochemically attached to a micron-sized glass or polystyrene bead that is then trapped. By attaching a single molecular motor (such as kinesin, myosin, RNA polymerase, etc) to such a bead, researchers have been able to probe motor properties such as: Does the motor take individual steps? What is the step size? How much force can the motor produce? Similarly, by attaching the beads to the ends of single pieces of DNA, experiments have measured the elasticity of the DNA, as well as the forces under which the DNA breaks or undergoes a phase transition. The Principle Behind the Operation of Optical Tweezers Figure 1b shows a more detailed look at how an optical trap works. The basic principle behind optical tweezers is the momentum transfer associated with bending light. Light carries momentum that is proportional to its energy and in the direction of propagation. Any change in the direction of light, by reflection or refraction, will result in a change of the momentum of the light. If an object bends the light, changing its momentum, conservation of momentum requires that the object must undergo an equal and opposite momentum change. This gives rise to a force acting on the object. What Happens When the Light from the Laser Interacts with the Polystyrene Bead In a typical optical tweezers set-up, the incoming light comes from a laser which has a "Gaussian intensity profile". Basically, the light at the center of the beam is brighter than the light at the edges. When this light interacts with a bead, the light rays are bent according to the laws of reflection and refraction (two example rays are shown in Figure 1b). Fscattering and Fgradient - Explaining How the Scattering Force and the Gradient Force Work The sum of the forces from all such rays can be split into two components: Fscattering, the scattering force, pointing in the direction of the incident light (z, see axes in Figure 1b), and Fgradient, the gradient force, arising from the gradient of the Gaussian intensity profile and pointing in x-y plane towards the center of the beam (dotted line). The gradient force is a restoring force that pulls the bead into the center. If the contribution to Fscattering of the refracted rays is larger than that of the reflected rays, then a restoring force is also created along the z-axis, and a stable trap will exist. Incidentally, the image of the bead can be projected onto a quadrant photodiode to measure nm-scale displacements. How the Restoring Force Bulls the Bead Back to the Center Whenever it is Displaced When the bead is displaced from the center of the trap, what force does it feel? The restoring force of the optical trap works like an optical spring: the force is proportional to the displacement out of the trap. In practice, the bead is constantly moving with Brownian motion. But whenever it leaves the center of the optical trap, the restoring force pulls it back to the center. If some external object, like a molecular motor, were to pull the bead away from the center of the trap, a restoring force would be imparted to the bead and thus to the motor. An example trace of a single kinesin motor taking 8 nm steps against a 5-pN force is shown in Figure 2. | 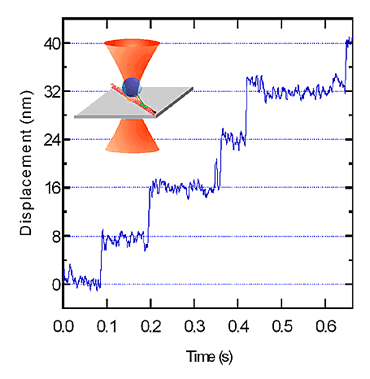
| | Figure 2. Measurement of the 8-nm steps of a single kinesin motor. | Modern Optical Tweezers In practice, optical tweezers are very expensive, custom-built instruments. These instruments usually start with a commercial optical microscope but add extensive modifications. In addition, the capability to couple multiple lasers into the microscope poses another challenge. High power infrared laser beams are often used to achieve high trapping stiffness with minimal photo-damage to biological samples. Precise steering of the optical trap is accomplished with lenses, mirrors, and acousto/electro-optical devices that can be controlled via computer. Figure 3 is meant to give an idea of the number of elements in such a system. In short, these are very complicated instruments that require a working knowledge of microscopy, optics, and laser techniques. | 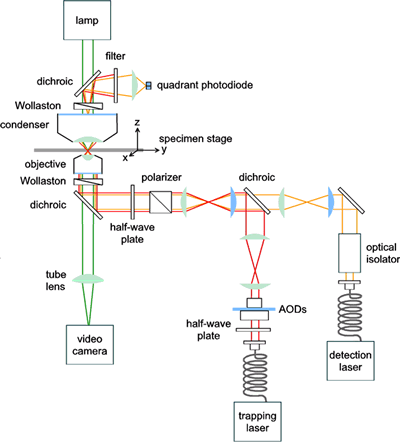
| | Figure 3. The typical set-up for modern optical tweezers. | Note: A complete list of references can be found by referring to the original text. |